O-Solution 时间频率解析功能 OS-0527
即使是FFT分析难以捕捉的瞬态现象, 也可以在保持频率分辨率的同时,清晰地展现出伴随着频率成分的时间变化。 它配备了两种类型的分析,短时傅里叶变换和小波变换。
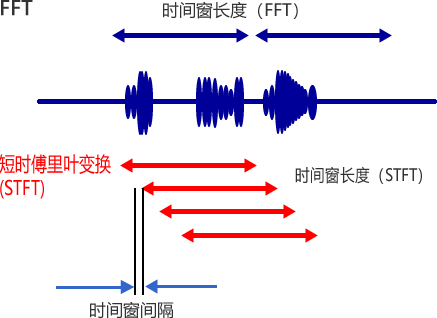
短时傅里叶变换 STFT (Short Time Fourier Transform)
可以在用户的指定条件(剪切时间窗长度和间隔)下进行傅里叶变换。 因此可以设置用户指定的任意剪切时间窗长度,这对于在很短的时间内观察频谱变化相当有效。
小波变换 (Wavelet transform)
这是一种可以同时分析复杂波形的时间波动和空间转移的分析方法,例如突发性或不稳定的声音和振动。 该方法根据频率改变分析时间的长度, 而且由于时间和频率非常平衡,所以可以有效地捕获整体的分析结果。
| 項目 | 短时傅里叶变换 | 小波变换 |
|---|---|---|
| 时间分辨率 | 固定的 | 高频率:高 低频率:低 |
| 频率分辨率 | 固定的 | 高频率:低 低频率:高 |
| 特长 | 是FFT分析的衍生版。 可以稳定地得到结果 |
时间分辨率与频率分辨率非常平衡。 |
| 弱势 | 提高时间分辨率以及频率分辨率以后,数据量会变大,计算时间也会变长。 | 可认知的频率不十分精确,稍显模糊。 |
时间频率解析实例 冲击性信号的分析
想要分析突发的震动波形。
如果只是用通常的FFT分析的话,时间分辨率太粗糙会导致不能进行更详细的分析。
但是利用短时傅里叶变换的话就能得到较高的频率分辨率与时间分辨率的结果。
| 型号 | 品名 | 数量 |
|---|---|---|
| OS-5100 | 系统平台 | 1 |
| OS-0522 | FFT分析功能 | 1 |
| OS-0527 | 时间频率解析功能 | 1 |
|
※需要能够录音的仪器装备(高功能声级计,FFT分析仪等等) |
||
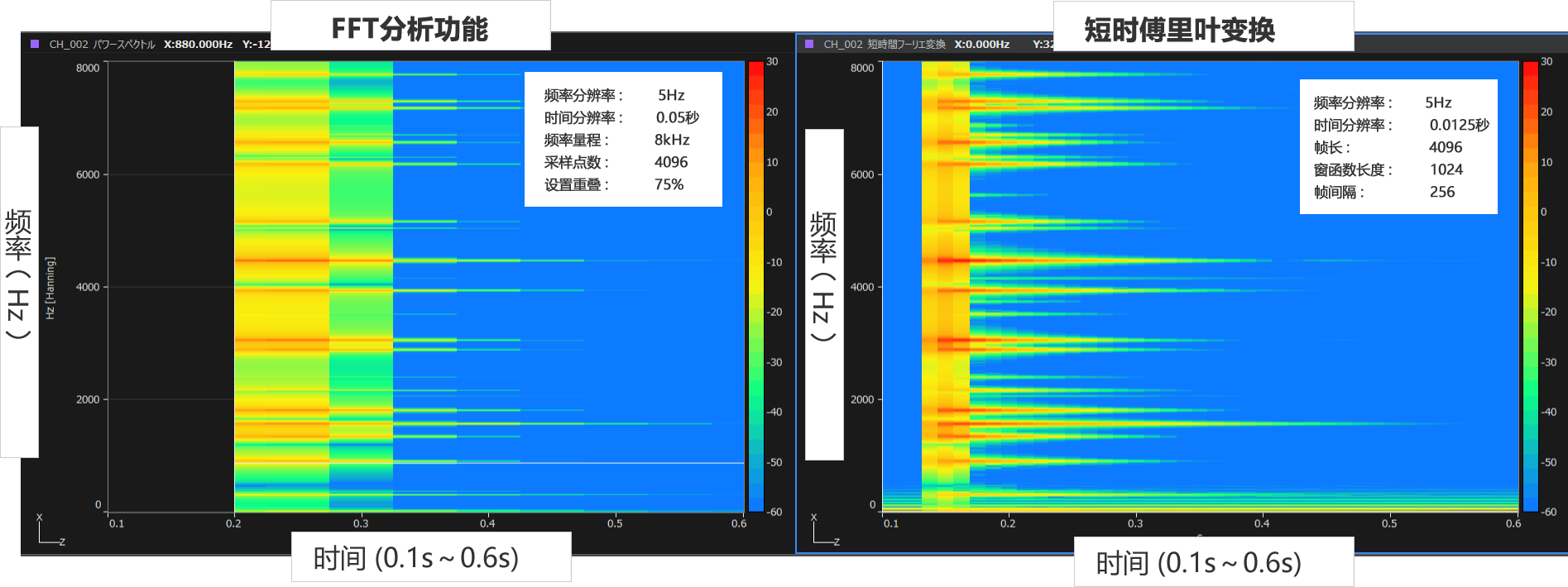
时间频率解析实例 高尔夫俱乐部的击球音的分析
以下介绍在较短时间内发生频率变化的高尔夫击球音的分析实例。
由于分析对象的信号的时间长度很短,如果使用FFT分析的话位于时间方向上的较细的频谱就会变得模糊(上左图)。
若使用短时傅里叶变换的话,即使帧的长度相同由于用户可以自由设定帧间隔与窗函数长度,
所以可以在维持频率分辨率的状态下将短时间内变化的频率成分鲜鲜明地展现出来(上右图)。
| 型号 | 品名 | 数量 |
|---|---|---|
| OS-5100 | 系统平台 | 1 |
| OS-0522 | FFT分析功能 | 1 |
| OS-0527 | 时间频率解析功能 | 1 |
|
※需要能够录音的仪器装备(高功能声级计,FFT分析仪等等) |
||

高尔夫的击球音 时间波形

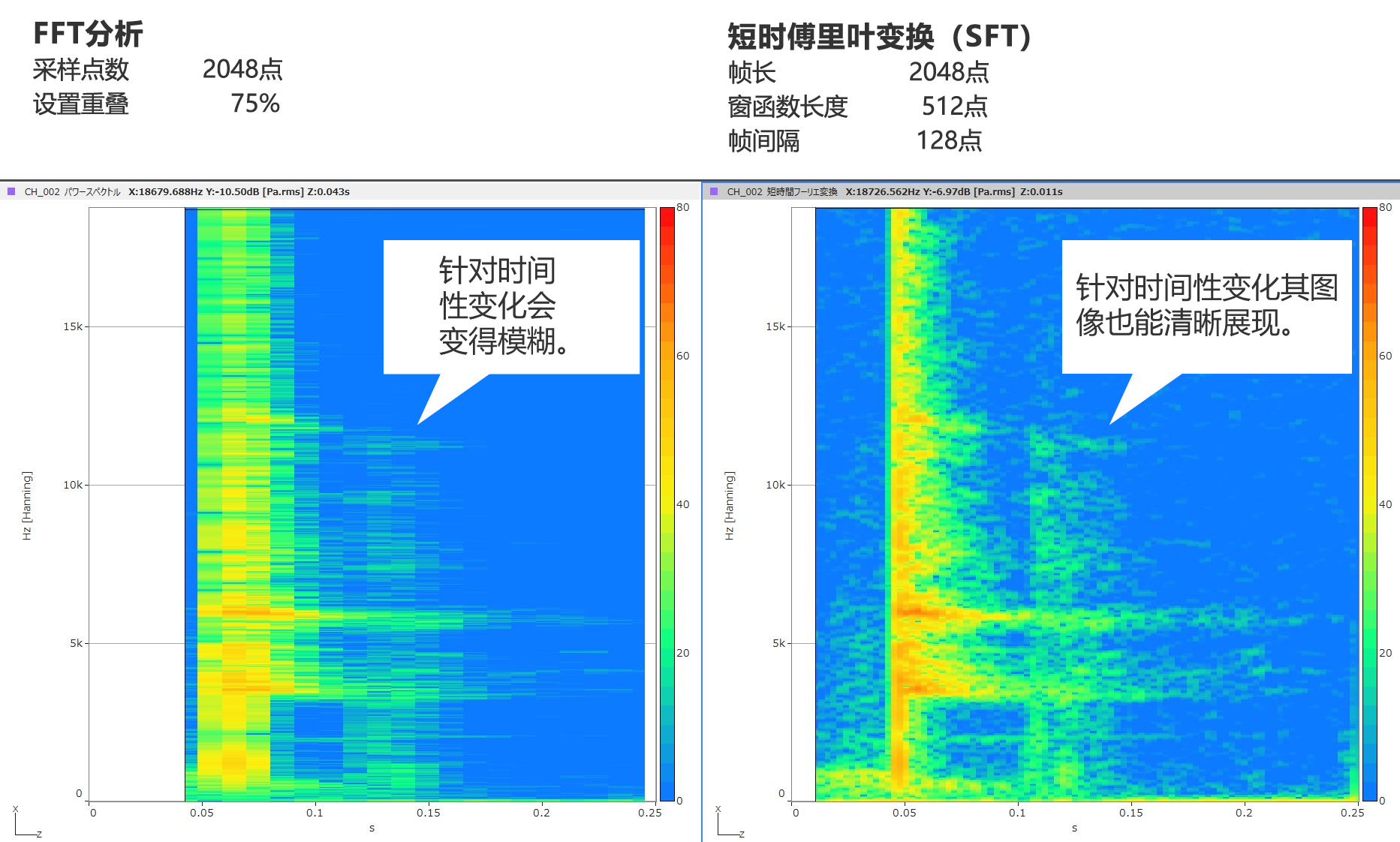
时间频率解析实例 机器运转声音的分析
以下是分析时间短且包含了机器运转声的异响的实例。
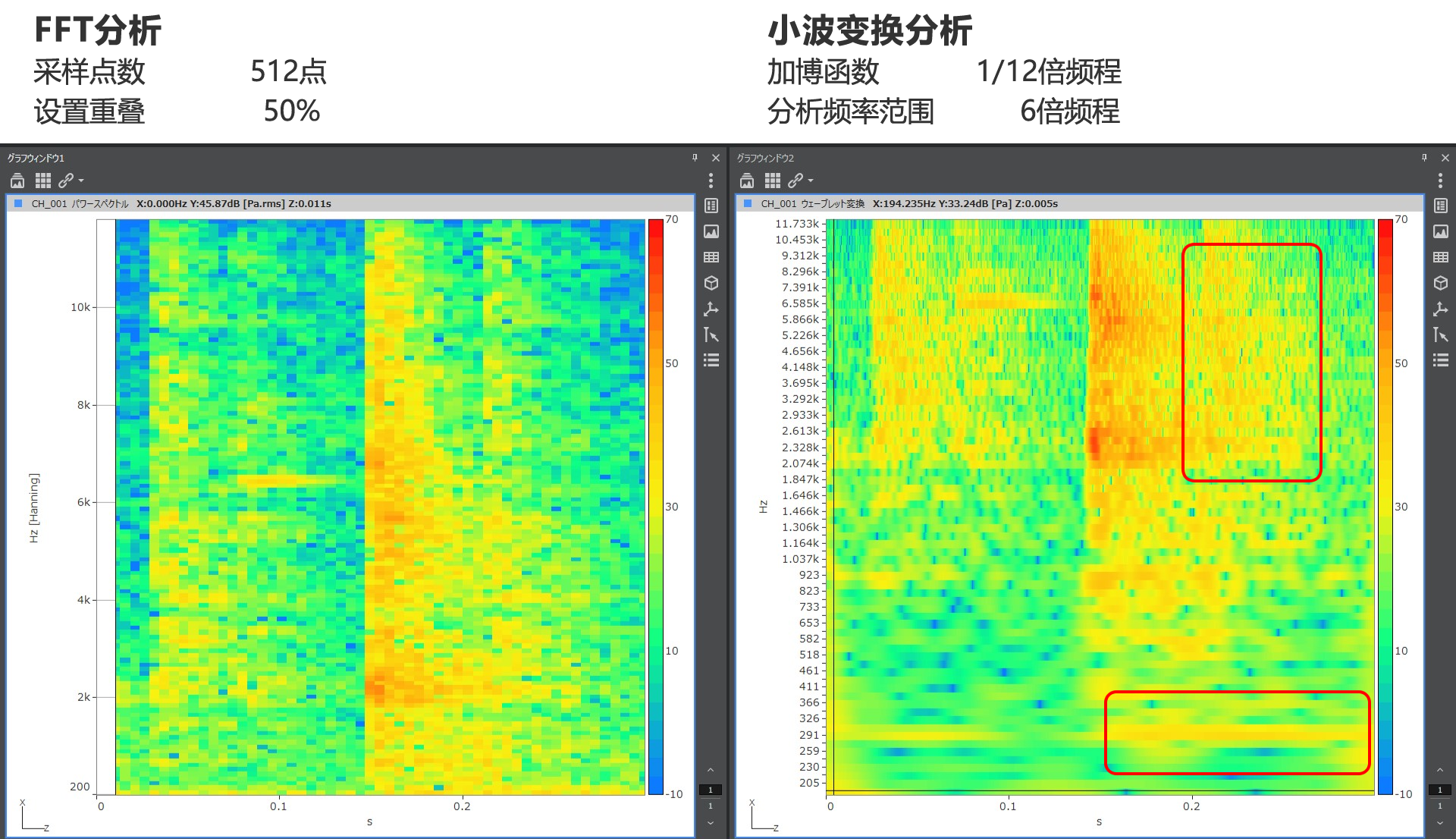
由于异响的频率成分的范围相当广泛,为了提高较低频率成分的分辨率,在进行FFT分析时有必要将帧数设置得大一点。
但是因为发生异响的时间非常短,所以有必要将帧数设置得短一点,但这样一来就得不到较好的频率分辨率和时间分辨率了(下左图)。
在这个实例中,用FFT分析会忽略掉的红色圆圈圈出来的成分(较低频率的成分)在换成小波变换之后就能可见了(下右图)。
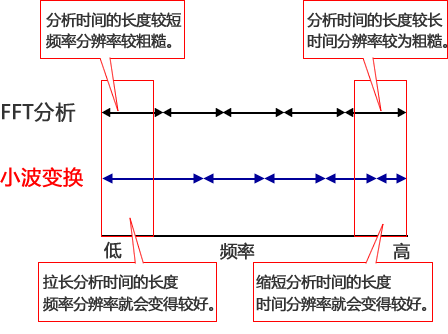
正如这样,小波变换能降低(频率分辨率足够高的)高频率成分的频率分辨率来提升时间分辨率,另一边也能降低较低频率成分(时间性变化较缓慢的)的时间分辨率来提高频率分辨率之后进行分析。
也就是说,这种分析方法与在声学分析中被广泛使用的N/1倍频程滤波器一样都是使用滤波器组的定比类型的分析。
| 型号 | 品名 | 数量 |
|---|---|---|
| OS-5100 | 系统平台 | 1 |
| OS-0522 | FFT分析功能 | 1 |
| OS-0527 | 时间频率解析功能 | 1 |
|
※需要能够录音的仪器装备(高功能声级计,FFT分析仪等等) |
||